Solitario FreeCell: ¡Juega gratis en línea, cómo jugar a FreeCell y más!
El Solitario original o clásico, también conocido como Patience, se remonta a siglos atrás. Ha seguido siendo un juego de salón popular hasta nuestros días, recuperando su popularidad tras el lanzamiento de Window 3.0 en 1990. A lo largo del siglo XX se desarrollaron diversas variantes del solitario: colocando las cartas de diversas maneras en el tablero. Entre estas innovaciones se encuentra el FreeCell. Al igual que las demás formas de solitario, FreeCell utiliza una baraja estándar de 52 cartas. Sin embargo, la diferencia radica en que las cartas se reparten boca arriba, en lugar de boca abajo. Para descubrir las maravillas de FreeCell, incluyendo las reglas de FreeCell y cómo se convirtió en uno de los juegos de cartas más populares de todos los tiempos, sigue leyendo. O bien, puedes ir al grano, desplazarte hacia arriba y jugar gratis a FreeCell online ahora mismo.
Si has dominado el juego clásico o variaciones como el Solitario Pirámide o el Solitario Spider, es hora de aprender a jugar al Solitario FreeCell. Está ampliamente considerado como el más difícil de todos.
Cómo jugar a FreeCell (Reglas fáciles de FreeCell)
Cómo ganar FreeCell
Antes de entrar en los detalles de cómo jugar al Solitario FreeCell, es esencial entender los objetivos. El objetivo es hacer cuatro montones de cada palo, cada uno con 13 cartas, en orden del as al rey. Estas cartas se colocan en los montones de base. Se gana cuando se reúnen los cuatro palos.
Reglas de FreeCell
Puede que estés familiarizado con la forma de jugar a FreeCell desde los primeros días de Windows, pero vamos a recapitular las reglas del Solitario FreeCell.
Encima de las cartas que has colocado, imagina ocho áreas vacías donde colocarás las cartas mientras juegas. Cuatro de ellas son las pilas de base, para cada palo, empezando por el as y terminando por el rey. Las otras cuatro son celdas libres; aquí podrás colocar una carta en espera, para liberar zonas del cuadro.
Para empezar, coloca las cartas que puedas en los montones de base, como se ha dicho, empezando por el as y llegando hasta el rey. Asegúrate de que no vas a necesitar una carta antes de colocarla en el montón de base, ya que es posible que no puedas recuperarla rápidamente.
Empieza a mover las cartas entre las columnas, creando montones de orden descendente y alternando los colores. Por ejemplo, un seis negro puede ir sobre un 7 rojo, o una reina roja sobre un rey negro. Si se abre una columna vacía en el tablero, puedes utilizarla como celda libre moviendo cartas al espacio libre. Intenta mover las cartas a los espacios libres de forma estratégica, para que sea más fácil crear pilas.
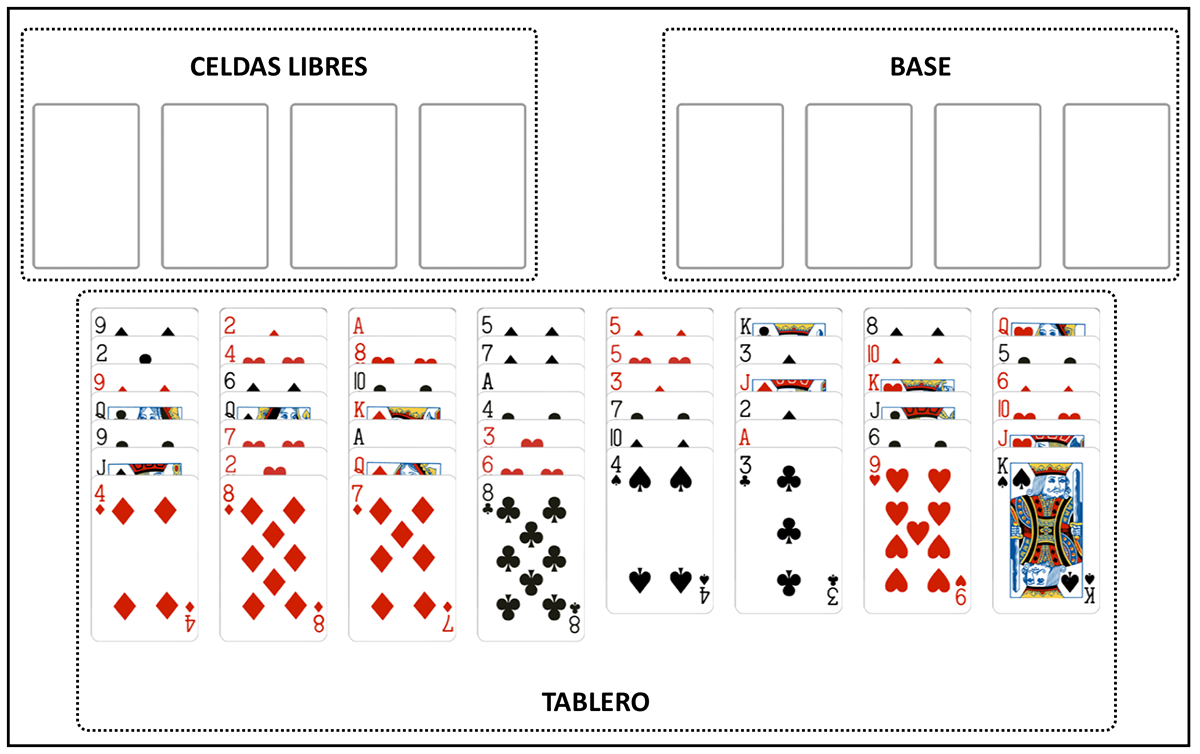
“Celdas libres” de FreeCell
Aquí es donde las cosas se complican. Puedes mover una sola carta a la vez, pero si quieres mover una secuencia de cartas, solo puedes hacerlo en proporción al número de celdas libres disponibles.
Cuatro casillas libres significan que puedes mover cinco cartas. Tres casillas libres significan que puedes mover cuatro cartas. Dos casillas libres significa que puedes mover tres cartas. Una libre significa que puedes mover dos cartas. Si todas las celdas libres están llenas, entonces solo puedes mover una carta.
Enhorabuena. Ya has aprendido a jugar al Solitario FreeCell. Es un juego de estrategia increíblemente complicado, pero no te preocupes si no siempre ganas, algunos repartos son imposibles de completar. Simplemente reparte otra serie de cartas y vuelve a intentar FreeCell.
No te olvides de jugar a nuestro juego gratuito de FreeCell más arriba. Jugar a FreeCell online te ahorra la molestia de configurar las cartas.
Cómo configurar el Solitario FreeCell
Al repartir las cartas, a diferencia del Solitario Clásico, en el que algunas cartas se colocan boca abajo, se repartirá todo el mazo boca arriba. Reparte ocho montones de cartas; los primeros cuatro montones contendrán siete cartas, los cuatro siguientes contendrán seis. Las columnas se denominan colectivamente tablero.
Al repartir las cartas, asegúrate de colocar cada carta superpuesta pero sin ocultar la carta de abajo.
FreeCell gratis
Puedes disfrutar jugando al Solitario FreeCell gratis en SOLITAIRE100.com. Funciona en cualquier navegador, en cualquier dispositivo y, lo más importante, ¡es totalmente gratis!
Historia de FreeCell
Los precursores
Aunque las versiones clásicas del solitario se remontan a los años 1700 y anteriores, FreeCell surgió probablemente a principios de 1900. Antes de la creación de FreeCell, hubo dos variantes tempranas que un día se convertirían en los juegos más queridos: Baker's Game y Eight Off. Este último juego, Eight Off, probablemente fue el primero, y se diferenciaba del FreeCell actual en que proporcionaba a los jugadores ocho depósitos en lugar de cuatro. Además, las columnas vacías solo se llenaban con un rey.
Martin Gardner, en la edición de junio de 1968 de Scientific American, describe el primero en su columna “Mathematical Games”. Había obtenido el juego de C. L. Baker, cuyo padre lo había aprendido de un inglés en la década de 1920 y luego lo había transmitido a su hijo. En esta nueva versión, el número de depósitos se reduce de ocho a cuatro y los jugadores pueden llenar las columnas vacías con cualquier secuencia de cartas, y no solo con un rey.
Incluso se ha sugerido que FreeCell se remonta a otro juego completamente distinto, conocido como Napoleón en Santa Elena. El juego procedía de Escandinavia, y se supone que tomó su nombre del hecho de que, durante su exilio en Santa Elena, Napoleón jugaba vorazmente al solitario. Un par de investigadores suecos descubrieron el juego y lo dataron al menos en 1945.
El único y verdadero
FreeCell, tal como lo conocemos y amamos hoy, no surgió hasta que Paul Alfille tuvo una idea genial. Dispuso las cartas en colores alternos, yendo hacia abajo en el tablero, imitando el Solitario Clásico. Alfille, estudiante de medicina por aquel entonces, quería averiguar las matemáticas que había detrás del juego y la probabilidad de conseguir un resultado perfecto. Además, odiaba barajar, y como el juego de Baker requería la clasificación de las cartas en palos, barajar llevaba mucho más tiempo. Como resultado de su cambio, casi todas las manos eran ganables, aunque algunas extremadamente difíciles. Además, ¡era mucho más fácil barajar!
Alfille codificó su nueva versión del juego utilizando el lenguaje de programación TUTOR para un sistema informático educativo PLATO en 1978. Incluso llegó a crear imágenes gráficas de las cartas utilizando la pantalla monocromática del sistema PLATO de 512x512. El sistema permitía a los jugadores competir en torneos, con complicados tratos específicos elegidos a mano para poner a prueba el ingenio de cada jugador.
Sin embargo, el juego seguía siendo un pasatiempo de nicho y poca gente conocía su existencia. No fue hasta que Jim Horne, que había aprendido el juego con el sistema PLATO, fue capaz de codificar el juego para Windows que las cosas despegaron - ¡aunque solo sea por la adición de gráficos en color!
Fama mundial
Siguiendo el trabajo de Jim Horne, una versión de FreeCell estuvo disponible en 1992 en el Microsoft Entertainment Pack 2, después de haberse incluido primero con Microsoft Win32s como programa de prueba. No sería hasta Windows 95 cuando FreeCell se hizo realmente popular entre el público. Microsoft lo incluyó entonces como parte de todos los sistemas Windows posteriores (excepto Windows Vista Business Edition, en el que había que instalarlo especialmente).
Después de que se hiciera ampliamente jugado y popular, aparecieron en el mercado muchas versiones alternativas de FreeCell. Sin embargo, la versión de FreeCell de 2003, que implementó características como la retracción de movimientos, sigue siendo la más popular.
A pesar de su tardío comienzo, FreeCell se ha convertido en una de las versiones más populares (si no la más popular) del solitario. En una encuesta realizada en el sitio Solitude, FreeCell ganó la votación con 824 votos de 4.000 respuestas.
¿Juegos de ordenador o computadoras de juego?
Naturalmente, muchos matemáticos y entusiastas de FreeCell se han lanzado a construir sus propios programas informáticos que pueden resolver automáticamente FreeCell.
En 1997, Don Woods creó un solucionador para FreeCell y otros juegos similares, que más tarde fue ampliado por Adrian Ettlinger y Wilson Callan, amalgamándose en el software FreeCell Pro. Más tarde, Tom Holroyd creó Patsolve, que utiliza movimientos atómicos; incluso se actualizó a una versión 3.0. Utilizando una función de ponderación derivada de los resultados de un algoritmo genético, el solucionador se hizo mucho más rápido.
Otros solucionadores han sido el 'Freecell Solver' de Shlomi Fish, que comenzó en el año 2000, y el solucionador de Gary Campbell para FreeCell, que era un programa pequeño y rápido, con un peso de 12 KB. Sin embargo, no fue hasta 2011, cuando los matemáticos desarrollaron un solucionador de FreeCell realmente impresionante en la Universidad Ben-Gurion del Negev en Israel. Sus resultados superaron a todos los mejores solucionadores hasta ese momento, mediante el uso de varias medidas heurísticas novedosas, así como algunos trucos matemáticos.
El resultado fue un solucionador, denominado GA-FreeCell, que redujo el tiempo de búsqueda en un 87%, el tiempo de solución en un 93% y la longitud de la solución en un 41%. Y lo que es más impresionante, GA-FreeCell fue capaz de completar el 98,36% de los juegos que intentó. De este modo, superó no solo a otro solucionador de FreeCell llamado HSDH (que consiguió un 96,43%), sino también a los tres mejores jugadores humanos del momento (97,61%, 96% y 66,4%).
Puede que no fuera Gary Kasparov contra Deep Blue, pero en el mundo de los juegos de cartas fue una gran noticia.
El Microsoft 32.000
En la versión original del Solitario de Microsoft, producida por Jim Horne, había 32.000 números repartidos. El juego numera cada trato, y luego un generador de números aleatorios escoge un trato al azar para cada jugada. En aquel momento, se pensaba que todos los repartos se podían resolver, al menos según un archivo de ayuda, que decía “Se cree (aunque no se ha demostrado) que todos los juegos se pueden ganar”. Sin embargo, después de Windows 95, dos tratos irresolubles se unieron a la mezcla, los números -1 y -2. Técnicamente, los 32.000 originales seguían siendo ganables. Aun así, Horne quería poner a prueba a los jugadores para ver si podían encontrar los dos repartos irresolubles.
Así comenzó el Proyecto FreeCell de Internet.
El proyecto FreeCell de Internet
En los primeros días de Internet, antes de que tuviéramos Snapchat o Facebook, YouTube o Reddit, Internet era un lugar más sencillo, era una época más simple. La gente se contentaba con pasar sus horas jugando al FreeCell buscando los juegos que no tenían solución. El esfuerzo había sido un caos hasta que Dave Ring se puso a trabajar organizando a los solucionadores humanos para aclarar cuáles, si es que había alguno, de los 32.000 repartos eran solucionables. A partir de agosto de 1994, se alistaron voluntarios de rec.puzzles, sci.math y otros sitios similares relacionados con los puzzles y las matemáticas. En total, se apuntaron 100 personas. A cada uno de los miembros de este equipo se le asignaron 100 acertijos consecutivos y se les informaba una vez que sus 100 acertijos habían sido resueltos o intentados. En ese momento, se encargaban de otros 100.
Si un asunto quedaba sin resolver, pasaba a los mejores solucionadores que Ring tenía disponibles. Poco a poco, el equipo se abrió camino a través de la pila de acuerdos. Resolviendo uno a uno, mediante el poder del multiprocesamiento. Sin embargo, los procesadores no eran chips de ordenador, sino cerebros humanos.
En octubre de 1995, habían resuelto todos los tratos de los 32.000. Todas menos una: El 11982; considerado irresoluble, a pesar de los esfuerzos de Ring y su equipo. Hasta la fecha, el 11982 sigue sin resolverse, habiendo sido abordado por miles de humanos y muchos programas informáticos.
Más tarde surgieron otros proyectos que pretendían analizar cuántos tratos eran resolubles. Un proyecto realizado por Don Woods en 1994 fue quizás el primer estudio estadístico a gran escala realizado con ordenadores. Examinó un millón de tratos al azar y, al año siguiente, informó que habían resuelto todos menos 14. De este modo, el juego tenía un porcentaje de victorias del 99,999%, que se compara favorablemente con el 75% del juego de Baker. ¡Alfille había tenido razón todo el tiempo!
El Gran Millón
En 2001, windows lanzó una versión actualizada de FreeCell, que incluía al menos 1.000.000 de repartos. Las 32.000 originales seguían intactas. Siguiendo el trabajo de los solucionadores Danny A. Jones y Gary D. Campbell, se ha revelado que del primer millón de juegos de FreeCell todos menos ocho son solucionables. Estos son: #11.982, #146.692, #186.216, #455.889, #495.505, #512.118, #517.776 y #781.948.
¿Qué tan difícil es FreeCell?
Ahora vamos a empezar a sumergirnos en las matemáticas que hay detrás del juego. No te preocupes, no es tan complicado como parece a primera vista.
En FreeCell, solo hay un número finito de repartos posibles, ya que con 52 cartas solo hay un número determinado de disposiciones en el tablero. Por eso, teóricamente, FreeCell es “NP-completo”. Esto significa que si se da un número limitado de partidas, un algoritmo puede resolver el juego utilizando una búsqueda de fuerza bruta para buscar problemas similares en “tiempo polinómico”. La prueba matemática de esto data del año 2000 y se publicó por primera vez en 2001.
Este tipo de problemas son un escollo importante en las matemáticas modernas. Consideremos un número primo. Son fáciles de identificar: basta con buscar un número que solo se divida por uno y por sí mismo, por ejemplo, 17. Pero, ¿hay alguna manera de identificar todos los números primos sin tener que contar cada número, preguntando si cada uno es un número primo?
De igual modo, ¿existe una forma de completar los juegos de FreeCell sin que el ordenador tenga que buscar entre todas las soluciones? Es fácil identificar una solución cuando se tiene una para comparar, pero ¿hay una manera de saber cómo completar el juego sin tener la respuesta? Si existiera un método rápido para averiguar la solución sin tener que comprobar todas las variaciones posibles, entonces revolucionaría el mundo tal y como lo conocemos.
Por eso, si alguien creara un programa para jugar al FreeCell que se ejecutara en tiempo polinómico, podría ganar el prestigioso Premio del Milenio del Instituto de Matemáticas Clay, dotado con la friolera de 1.000.000 de dólares. A pesar de la gran cantidad de dinero del premio, la mayoría de los investigadores no creen que exista una solución fácil.
¿Cómo hacer el juego más desafiante?
Uno de los principales inconvenientes de FreeCell es que, una vez que el jugador ha adquirido suficiente experiencia, un gran porcentaje de los repartos se vuelven bastante fáciles. Por ello, existen variaciones del juego: las dos variantes son los juegos precursores de Eight Off y Baker's Game. No obstante, incluso la versión inicial codificada por Alfille permitía a los jugadores ajustar el número de columnas que jugaban, de 4 a 10, con 1 a 10 casillas libres. Sin embargo, esto hace que algunos juegos sean imposibles.
Al aumentar el número de columnas, disminuye el número de casillas libres que se necesitan para ganar. Sin embargo, al disminuir el número de columnas, el juego se vuelve progresivamente más difícil. Otros jugadores han intentado el juego usando menos celdas libres, sin embargo, con menos celdas libres, se disminuye la posibilidad de poder completar el juego. Con tres casillas libres, la mayoría de las partidas se pueden ganar; sin embargo, con solo dos casillas libres, el porcentaje de victorias se sitúa en torno al 80%.
En la actualidad, existen algunas ofertas en las que un jugador puede completar el juego sin utilizar una casilla libre. No obstante, éstas son extraordinariamente raras. Incluso es posible que no tenga ningún movimiento en la posición inicial.
En una versión de FreeCell, conocida como Ephemeral FreeCell, los jugadores tienen 13 columnas con una única celda libre que solo se utiliza una vez. De ahí su nombre.
También hay un juego llamado Bonus FreeCell, que es más bien una versión de Eight Off, pero con empaquetamiento alternativo. También se pueden jugar variaciones en las que se reparten las cartas boca abajo. Sin embargo, los entusiastas de FreeCell suelen considerar estas variantes del Solitario Clásico, ya que el sello de FreeCell es que las cartas están todas boca arriba. Prueba a jugar a ForeCell, un precursor de FreeCell. En esta versión, se rellenan las casillas libres al principio de la partida.
Por último, está Seahaven Towers, que también se parece a Eight Off. La diferencia es que en Seahaven Towers, tienes diez columnas de cinco cartas. Las dos últimas cartas restantes se colocan en dos de las cuatro celdas libres disponibles.
Consejos y trucos
Ahora que conoces la apasionante historia de uno de los juegos de cartas más difíciles que existen, estarás deseando empezar a jugar a FreeCell online gratis. Pero antes de hacerlo, considera aprender algunos consejos y trucos. FreeCell requiere una cantidad increíble de habilidad, y con la mayoría de los juegos que se pueden resolver, todo lo que se necesita es un poco de paciencia y astucia para completar los tratos.
Por ello, hemos reunido seis consejos esenciales que debes recordar cuando juegues a FreeCell online o cuando juegues con cartas.
1. Examinar el cuadro
Antes de salir por las puertas, mover las cartas y llenar tus celdas libres, tómate un momento para examinar el cuadro. ¿Dónde están las cartas que podrías necesitar? Intenta jugar con varias jugadas por delante, ya que jugar la jugada obvia no siempre es la mejor opción.
2. Libera tus ases y dos
En cuanto puedas, coloca tus ases y dos en las casillas de origen. Cuanto más arriba estén, más prioritario será liberarlos.
3. Mantén tus celdas libres vacías
Si es posible, mantén tus celdas libres vacías, utilizándolas solo como último recurso. Las casillas libres limitarán naturalmente su capacidad de maniobra, restringiendo el número de cartas que se puede mover. Por lo tanto, antes de colocar una carta en una celda libre, asegúrate de agotar todas las demás posibilidades.
4. Crear una columna vacía
Mientras que una celda libre solo puede almacenar una carta, puede utilizar una columna vacía para almacenar una secuencia completa de cartas. Por lo tanto, al abrir una columna vacía, crea muchas posibilidades.
5. Llenar las columnas con reyes
Los reyes son la carta más alta en FreeCell. Por lo tanto, llenar una columna vacía con un rey te permitirá crear largas secuencias que no necesitarás mover después.
6. No muevas automáticamente las cartas a las celdas de origen
Puede parecer un instinto mover las cartas a las casillas de origen. Ese es el objetivo, ¿verdad? Sin embargo, puede que necesites esas cartas más adelante, por lo tanto, mantenlas en juego durante el tiempo que las necesites para mover las cartas de rango inferior.
Ahí lo tienes. La extensa historia de FreeCell. Consejos y trucos. La matemática detrás de la magia.
Ahora solo queda una cosa por hacer: ¡empezar a jugar al Solitario FreeCell gratis!
Fuentes:
https://en.wikipedia.org
https://www.mentalfloss.com
https://cards.fandom.com
http://plrplr.com
http://www.genetic-programming.org