Pasjans FreeCell: Graj za darmo online, jak grać w FreeCell i wiele więcej!
Pasjans oryginalny lub klasyczny, znany również jako Patience, z francuskiego „Cierpliwość”, pochodzi sprzed wielu wieków. Pozostał on popularną grą towarzyską aż do współczesności, odzyskując popularność po wydaniu Windows 3.0 w 1990 roku. W XX wieku opracowano kilka wariantów pasjansa: poprzez układanie kart na różne sposoby na planszy. Wśród tych innowacji był FreeCell. Podobnie jak wszystkie inne formy pasjansa, FreeCell korzysta ze standardowej talii 52 kart. Jednak różnica polega na grze, w której karty są raczej odkryte, a nie zakryte. Aby odkryć cuda gry FreeCell, w tym zasady gry FreeCell i dowiedzieć się, jak stała się jedną z najpopularniejszych gier karcianych wszechczasów, czytaj dalej. Albo przejdź do sedna, przewiń w górę i zagraj w darmową grę FreeCell online już teraz!
Jeśli opanowałeś już klasyczną grę lub jej odmiany, takie jak Pasjans Piramida lub Pasjans Pająk, czas nauczyć się grać w Pasjansa FreeCell. Powszechnie uważa się, że jest najtrudniejszy z nich wszystkich.
Jak grać w FreeCell (proste zasady gry w FreeCell)
Zawęziliśmy podstawy gry FreeCell.
Jak wygrać w FreeCell
Zanim przejdziemy do szczegółów Pasjansa FreeCell, konieczne jest zrozumienie celów tej gry. Celem jest ułożenie czterech stosów z każdego koloru, każdy po 13 kart, w kolejności od asa do króla. Te karty należy odłożyć na stosy bazowe. Wygrywasz, gdy wszystkie cztery kolory zostaną ułożone.
Zasady gry w Pasjansa FreeCell
Być może wiesz, jak grać w FreeCell od wczesnych dni Windowsa, ale podsumujmy zasady gry w Pasjansa FreeCell.
Nad kartami, które rozłożyłeś, wyobraź sobie osiem pustych obszarów, w których będziesz układać karty podczas gry. Cztery z nich to Twoje stosy bazowe dla każdego koloru, zaczynając od asa, a kończąc na królu. Pozostałe cztery to wolne komórki; tutaj będziesz mógł tymczasowo przechować kartę, aby zwolnić obszary na planszy.
Na początek umieść dowolne karty w stosach bazowych, jak opisano powyżej, zaczynając od asa i przechodząc do króla. Upewnij się, że nie będziesz potrzebować karty przed umieszczeniem jej na stosie bazowym, ponieważ możesz nie być w stanie szybko jej odzyskać.
Zacznij przenosić karty między kolumnami, tworząc stosy w kolejności malejącej i na przemian z kolorami. Na przykład czarna szóstka może trafić na czerwoną siódemkę lub czerwona dama na czarnego króla.
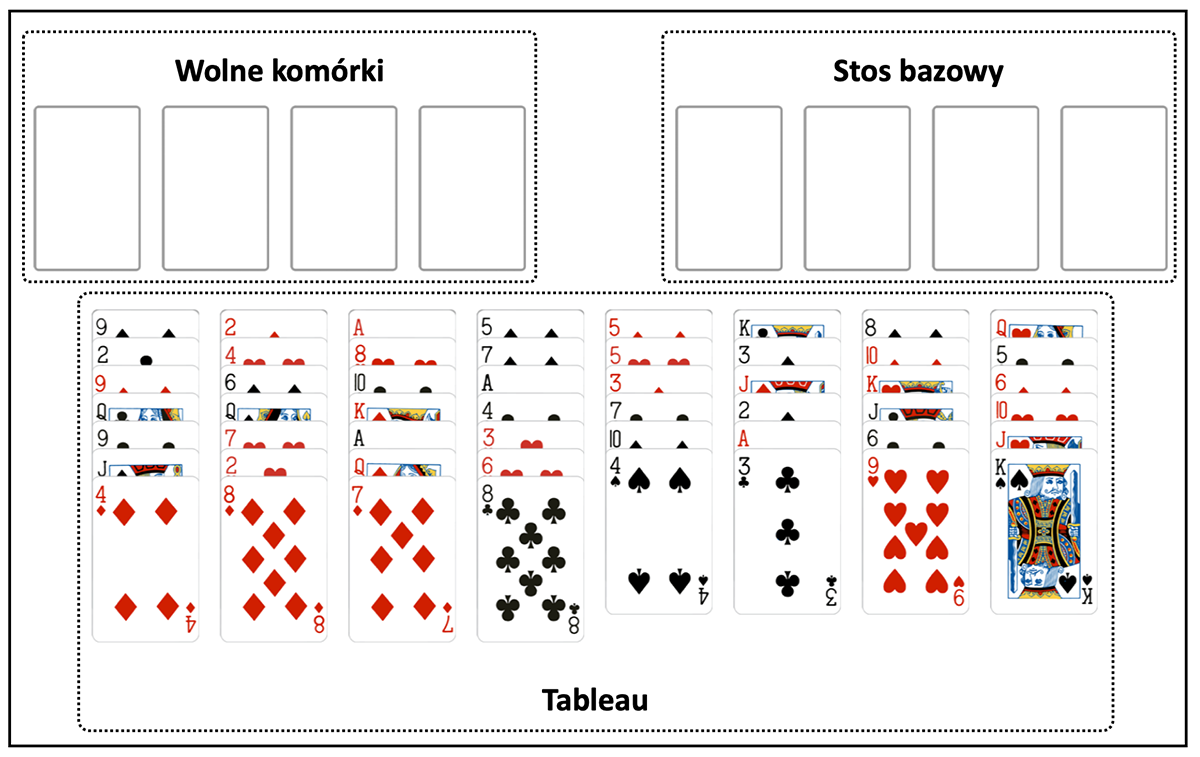
Wolne komórki w FreeCell
Tutaj sprawy się komplikują. Możesz przenosić pojedynczą kartę na raz, ale jeśli chcesz przenieść sekwencję kart, możesz to zrobić tylko proporcjonalnie do liczby dostępnych wolnych komórek.
Cztery wolne komórki oznaczają, że możesz przenieść pięć kart.
Trzy puste wolne komórki oznaczają, że możesz przenieść cztery karty.
Dwie wolne komórki oznaczają, że możesz przenieść trzy karty.
Jedna wolna komórka oznacza, że możesz przenieść dwie karty.
Jeśli wszystkie wolne komórki są pełne, możesz przenieść tylko jedną kartę.
Gratulacje! Wiesz już, jak grać w Pasjansa FreeCell. To niesamowicie trudna gra strategiczna, ale nie martw się, jeśli rzadko wygrywasz, niektóre rozdania są niemożliwe do wykonania. Po prostu rozdaj kolejną talię kart i zagraj ponownie w FreeCell.
Nie zapomnij zagrać w naszą bezpłatną grę FreeCell powyżej! Gra FreeCell online oszczędzi Ci kłopotów z ułożeniem kart.
Jak ułożyć Pasjansa FreeCell
Podczas rozdawania kart, w przeciwieństwie do Pasjansa Klasycznego, w którym niektóre karty są zakryte, rozdajesz całą talię odkrytą. Rozdaj osiem stosów kart; pierwsze cztery stosy będą zawierały po siedem kart, następne cztery po sześć. Kolumny są wspólnie nazywane tableau.
Podczas rozdawania kart upewnij się, że każda karta nakłada się na siebie, ale nie zakrywa karty poniżej.
FreeCell za free
Możesz grać w darmowego pasjansa FreeCell na SOLITAIRE100.com. Działa w każdej przeglądarce, na każdym urządzeniu, a co najważniejsze - całkowicie za darmo!
Historia FreeCell
Prekursorzy
Chociaż klasyczne wersje pasjansa pochodzą z XVIII wieku, FreeCell prawdopodobnie powstał na początku XX wieku. Przed stworzeniem FreeCell istniały dwa wczesne warianty, które pewnego dnia stały się popularnymi grami: Baker's Game i Eight Off. Ostatnia gra, Eight Off, prawdopodobnie pojawiła się jako pierwsza, różniąc się od współczesnego FreeCell poprzez oferowanie graczom osiem magazynów zamiast czterech. Dodatkowo puste kolumny były wypełnione tylko królem.
Martin Gardner w wydaniu Scientific American z czerwca 1968 r. pierwszy raz opisuje to w swojej rubryce „Gry Matematyczne”. Poznał tę grę od C. L. Bakera, którego ojciec nauczył się jej od Anglika w latach dwudziestych XX wieku, a następnie przekazał ją swojemu synowi. W nowej wersji liczba magazynów zmniejsza się z ośmiu do czterech, a gracze mogą wypełnić puste kolumny dowolnym rzędem kart, a nie tylko królem.
Pojawiły się nawet sugestie, że FreeCell wywodzi się całkowicie z innej gry, znanej jako „Napoleon na Św. Helenie”. Gra pochodzi ze Skandynawii i prawdopodobnie wzięła swoją nazwę od faktu, że podczas wygnania na Wyspie Świętej Heleny, Napoleon zachłannie grał w pasjansa. Para szwedzkich badaczy odkryła tę grę i datuje ją na co najmniej 1945 rok.
Jedyny w swoim rodzaju
FreeCell, jaki znamy i kochamy dzisiaj, powstał dopiero, gdy Paul Alfille wpadł na genialny pomysł. Ułożył karty na przemian z kolorami, malejąco na planszy, odzwierciedlając Pasjans Klasyczny. Alfille, ówczesny student medycyny, chciał obliczyć matematykę stojącą za grą i prawdopodobieństwo osiągnięcia doskonałego wyniku. Co więcej, nienawidził tasowania, a ponieważ gra Bakera wymagała sortowania kart w kolory, tasowanie trwało znacznie dłużej.
W wyniku jego zmiany prawie każde rozdanie było możliwe do wygrania, choć niektóre były niezwykle trudne. Poza tym tasowanie było o wiele łatwiejsze!
Alfille zakodował swoją nową wersję gry w języku programowania TUTOR dla edukacyjnego systemu komputerowego PLATO w 1978 roku. Posunął się nawet do stworzenia graficznych obrazów kart do gry, korzystając z monochromatycznego wyświetlacza systemu PLATO 512x512. System umożliwiał graczom na udział w turniejach, w których specyficzne, złożone, ręcznie dobierane układy sprawdzały inteligencję każdego gracza.
Jednak gra pozostała niszowym hobby i niewiele osób było świadomych jej istnienia. Dopiero Jim Horne, który poznał grę dzięki systemowi PLATO, był w stanie zakodować ją dla systemu Windows, sprawy nabrały tempa - choćby tylko po to, by dodać kolorową grafikę!
Światowa sława
W następstwie pracy Jima Horne'a wersja FreeCell została udostępniona w 1992 roku w pakiecie Microsoft Entertainment Pack 2, po tym jak została po raz pierwszy dołączona do Microsoft Win32 jako program testowy. Dopiero w systemie Windows 95 gra stała się naprawdę popularna wśród społeczeństwa. Microsoft włączył ją następnie do wszystkich późniejszych systemów Windows (z wyjątkiem Windows Vista Business Edition, gdzie musiał być oddzielnie zainstalowany).
Po jej wydaniu i zdobyciu popularności, na rynku pojawiło się wiele alternatywnych wersji FreeCell. Jednak najpopularniejsza pozostaje wersja FreeCell z 2003 roku, w której wprowadzono takie funkcje, jak cofanie ruchów.
Pomimo późnego startu, FreeCell stał się jedną z najpopularniejszych (jeśli nie najpopularniejszą) wersji pasjansa. W ankiecie przeprowadzonej na stronie Solitude, FreeCell wygrał głosowanie, uzyskując 824 głosy spośród 4000 odpowiedzi.
Gry komputerowe czy komputery do grania?
Oczywiście wielu matematyków i entuzjastów FreeCell zaczęło tworzyć własne programy komputerowe, które mogły automatycznie rozwiązywać FreeCell.
W 1997 roku Don Woods stworzył urządzenie do rozwiązywania FreeCell i innych podobnych gier, który zostało później rozbudowane przez Adriana Ettlingera i Wilsona Callana, stając się oprogramowaniem FreeCell Pro. Później Tom Holroyd stworzył Patsolve, program wykorzystujący ruchy atomowe; zaktualizował go nawet do wersji 3.0. Wykorzystując funkcję wagową pochodzącą z wyników algorytmu genetycznego, urządzenie stało się znacznie szybsze.
Inne podobne urządzenia to „Freecell Solver” Shlomi Fisha, które powstało w 2000 roku, oraz urządzenie Gary'ego Campbella dla FreeCell, które było małym i szybkim programem o wadze 12 KB. Jednak dopiero w 2011 roku matematycy opracowali naprawdę imponujące urządzenie do rozwiązywania FreeCell na Uniwersytecie Ben-Guriona w Negev w Izraelu. Ich wyniki przewyższały wszystkie najlepsze rozwiązania do tej pory, dzięki zastosowaniu kilku nowatorskich środków heurystycznych, a także szczypty matematycznej magii.
W rezultacie powstał system, nazwany GA-FreeCell, który skrócił czas wyszukiwania o 87%, czas rozwiązania o 93%, a długość o 41%. Jeszcze bardziej imponujące było to, że GA-FreeCell był w stanie ukończyć 98,36% wszystkich rozpoczętych gier, których się podejmował. W związku z tym wyprzedzał nie tylko inny system do FreeCell o nazwie HSDH (który zdobył 96,43%), ale także trzech najlepszych graczy z tamtych lat (97,61%, 96% i 66,4%).
Może nie był to mecz Gary’ego Kasparowa przeciwko Deep Blue, ale w świecie gier karcianych to było coś wielkiego!
Microsoft 32000
W oryginalnej wersji Microsoft Solitaire wyprodukowanej przez Jima Horne'a było 32 000 rozdań. Gra liczy każde rozdanie, a następnie generator liczb losowych wybiera losowe rozdanie dla każdej gry. W tamtym czasie uważano, że wszystkie rozdania można rozwiązać, przynajmniej według pliku pomocy, który brzmiał: „Uważa się (choć nie udowodniono), że każdą grę można wygrać”. Jednak po Windows 95 do mieszanki dołączyły dwie nierozwiązywalne rozdania, numery -1 i -2. Technicznie rzecz biorąc, pierwsze 32 000 rozdań wciąż było do wygrania. Mimo to Horne chciał przetestować graczy, aby sprawdzić, czy uda im się znaleźć dwa nierozwiązywalne rozdania.
W ten sposób rozpoczął się projekt Internet FreeCell.
Projekt Internet FreeCell
W początkach Internetu, zanim mieliśmy Snapchata lub Facebooka, YouTube czy Reddit, Internet był znacznie prostszym miejscem. Ludzie cieszyli się z niezliczonych godzin rozegranych w FreeCell, szukając nierozwiązywalnych gier. Wysiłki te były daremne, dopóki Dave Ring nie zaczął korzystać z ludzkich rozwiązujących, aby wyjaśnić, które z 32 000 rozdań, jeśli w ogóle, można rozwiązać. Od sierpnia 1994 roku ochotnicy zapisywali się na stronach rec.puzzles, sci.math i innych podobnych witrynach z zagadkami i matematyką. W sumie zapisało się 100 osób. Ta różnorodna ekipa otrzymała 100 kolejnych rozdań i musiała złożyć raport po rozwiązaniu lub próbie ich rozwiązania. W tym momencie dostawali kolejne 100.
Jeśli rozdanie pozostało nierozwiązane, przechodziło w ręce najlepszych rozwiązujących, jakimi dysponował Ring. Powoli, ale pewnie, zespół pracował nad stosem rozdań, rozwiązując je jeden po drugim, wykorzystując moc przetwarzania wieloprocesowego. Procesorami nie były jednak czipy komputerowe, lecz ludzkie mózgi.
Do października 1995 roku rozwiązali wszystkie rozdania spośród 32 000. Wszystkie z wyjątkiem jednego: 11982, uznanego za nierozwiązywalne, pomimo wszelkich starań Ringa i jego zespołu. Do tej pory problem 11982 pozostaje nierozwiązany, choć zajęło się nim już tysiące ludzi i wiele programów komputerowych. Później pojawiły się inne projekty, których celem było przeanalizowanie, ile rozdań można było rozwiązać. Projekt Dona Woodsa z 1994 roku był prawdopodobnie pierwszym badaniem statystycznym na dużą skalę, w którym wykorzystano komputery. Zbadał milion losowych rozdań, zgłaszając w następnym roku, że rozwiązali wszystkie z wyjątkiem 14. W ten sposób gra uzyskała współczynnik wygranych na poziomie 99,999% i znacznie przewyższył 75% skuteczności Baker Game. Alfille przez cały czas miał rację!
Wielki milion
W 2001 roku Windows wypuścił zaktualizowaną wersję FreeCell, zawierającą co najmniej 1,000,000 rozdań. Oryginalne 32 000 było nadal nienaruszone. W następstwie pracy dwóch rozwiązujących, Danny'ego A. Jonesa i Gary'ego D. Campbella, okazało się, że z pierwszego miliona gier FreeCell wszystkie oprócz ośmiu można rozwiązać. Są to: #11,982, #146,692, #186,216, #455,889, #495,505, #512,118, #517,776, oraz #781,948.
Jak trudny jest FreeCell?
Teraz zacznijmy zagłębiać się w matematykę gry. Spokojnie, to nie takie skomplikowane, jak się może wydawać.
W grze FreeCell istnieje tylko ograniczona liczba rozdań, ponieważ przy 52 kartach możliwa jest tylko określona liczba kombinacji na planszy. Dlatego też, teoretycznie, FreeCell jest „NP-kompletny”. Oznacza to, że jeśli dana jest ograniczona liczba rozgrywek, algorytm może rozwiązać grę, używając przeszukiwania siłowego w celu znalezienia podobnych problemów w „czasie wielomianowym”. Matematyczny dowód na to datuje się na rok 2000 i został po raz pierwszy opublikowany w 2001 roku.
Takie problemy są główną przeszkodą we współczesnej matematyce. Rozważ liczbę pierwszą. Są one na ogół łatwe do rozpoznania: wystarczy poszukać liczby, która dzieli się tylko przez jeden i samą siebie, np. 17. Ale czy istnieje sposób na zidentyfikowanie wszystkich liczb pierwszych bez konieczności liczenia każdej z nich, pytając, czy każda z nich jest liczbą pierwszą?
Podobnie, czy istnieje sposób na ukończenie gier FreeCell bez konieczności przeszukiwania wszystkich rozwiązań na komputerze? Łatwo jest znaleźć rozwiązanie, gdy masz je porównać, ale czy istnieje sposób, aby dowiedzieć się, jak ukończyć grę bez odpowiedzi? Gdyby istniał szybki sposób na wypracowanie rozwiązania bez konieczności sprawdzania wszystkich możliwych wariantów, zrewolucjonizowałoby to świat, jaki znamy.
Gdyby ktoś stworzył program do gry FreeCell, który działałby w czasie wielomianowym, mógłby zdobyć prestiżową nagrodę Millenium Prize przyznawaną przez Clay Mathematics Institute (Instytut Matematyki Clay) o wartości $1,000,000. Pomimo ogromnej nagrody pieniężnej, większość badaczy nie wierzy, że istnieje jakiekolwiek proste rozwiązanie.
Jak sprawić, by gra była bardziej wymagająca?
Jedną z głównych wad gry FreeCell jest to, że gdy gracz zdobędzie wystarczające doświadczenie, duży procent rozdań staje się dość łatwy. Dlatego istnieją warianty tej gry: te dwa warianty są prekursorami gier Eight Off i Baker's Game. Jednak nawet początkowa wersja zakodowana przez Alfille pozwalała graczom na dostosowanie liczby kolumn, którymi grali, w zakresie od 4 do 10, z 1 do 10 wolnych komórek. Jednak to sprawia, że niektóre rozdania są niemożliwe.
Zwiększając liczbę kolumn, spada liczba wolnych komórek potrzebnych do wygrania. Jednak zmniejszając liczbę kolumn, gra staje się coraz trudniejsza. Inni gracze próbowali grać przy użyciu mniejszej liczby wolnych komórek, jednak przy mniejszej liczbie wolnych komórek zmniejszasz możliwość ukończenia gry. Dzięki trzem wolnym komórkom w większości gier nadal można wygrać; jednak przy tylko dwóch wolnych komórkach współczynnik wygranych wynosi około 80%.
Obecnie istnieje kilka rozdań, w których gracz może ukończyć grę bez korzystania z wolnej komórki. Są one jednak niezwykle rzadkie. Możesz nawet nie mieć żadnych ruchów już w pozycji wyjściowej.
W jednej wersji FreeCell, znanej jako Ephemeral FreeCell, gracze mają 13 kolumn z pojedynczą wolną komórką, która jest używana tylko raz. Stąd jej nazwa.
Istnieje również gra o nazwie Bonus FreeCell, która jest bardziej wersją Eight Off, ale z alternatywnym opakowaniem. Możesz także grać w odmiany, w których rozdajesz karty zakryte. Jednak entuzjaści FreeCell często uważają je za odmiany Pasjansa Klasycznego, ponieważ cechą charakterystyczną FreeCell jest to, że wszystkie karty są odkryte. Spróbuj swoich sił w ForeCell, wczesnym prekursorze FreeCell. W tej wersji wypełniasz wolne komórki na początku gry.
I na koniec, Seahaven Towers, które również przypomina Eight Off. Różnica polega na tym, że w Seahaven Towers masz dziesięć kolumn po pięć kart. Ostatnie dwie pozostałe karty są umieszczane w dwóch z czterech dostępnych wolnych komórek.
Wskazówki i porady
Teraz znasz już ekscytującą historię jednej z najtrudniejszych gier karcianych, z niecierpliwością pewnie czekasz na darmową grę FreeCell online. Jednak zanim to zrobisz, zapoznaj się z kilkoma wskazówkami i poradami. FreeCell wymaga niesamowitych umiejętności, a ponieważ większość gier można rozwiązać, wystarczy odrobina cierpliwości i sprytu, aby zakończyć rozdanie.
Dlatego zebraliśmy sześć głównych wskazówek, o których należy pamiętać, grając w grę FreeCell online lub inne gry karciane.
1. Przeanalizuj tableau
Zanim wyskoczysz z przesuwaniem kart i wypełnianiem wolnych komórek, poświęć chwilę na zbadanie planszy. Gdzie są karty, których możesz potrzebować? Spróbuj zagrać kilka ruchów do przodu, ponieważ zagranie oczywistego ruchu nie zawsze jest najlepszym rozwiązaniem.
2. Uwolnij swoje asy i dwójki
Tak szybko, jak to możliwe, umieść swoje asy i 2 w komórkach docelowych. Im wyżej się znajdują się w kolumnach, tym wyższy powinien być priorytet ich usunięcia.
3. Zachowaj wolne komórki puste
W razie możliwości, pozostaw wolne komórki puste, używając ich tylko w ostateczności. Wolne komórki w naturalny sposób ograniczą twoją manewrowość, ograniczając liczbę kart, które możesz przenieść. Dlatego przed umieszczeniem karty w wolnej komórce upewnij się, że wyczerpałeś wszystkie inne możliwości.
4. Utwórz pustą kolumnę
Tam, gdzie wolna komórka może przechowywać tylko jedną kartę, możesz użyć pustej kolumny do przechowywania całej sekwencji kart. Dlatego uwalniając kolumnę, stwarzasz wiele możliwości.
5. Wypełnij kolumny królami
Królowie są najwyższymi kartami w grze FreeCell. Dlatego wypełnienie pustej kolumny królem pozwoli Ci utworzyć długie sekwencje, których nie będziesz musiał później przenosić.
6. Nie przenoś automatycznie kart do komórek docelowych
Przenoszenie kart do komórek docelowych zdaje się być instynktowne. Taki jest cel gry, prawda? Możesz jednak potrzebować tych kart później, dlatego zachowaj je w grze tak długo, jak potrzebujesz, aby przenieść karty o niższej randze.
No i proszę, oto ona. Rozległa historia FreeCell. Porady i wskazówki. Matematyka kryjąca się za magią.
Teraz pozostaje tylko jedno: zacznij grać w darmowego Pasjansa FreeCell!
Źródła:
https://en.wikipedia.org
https://www.mentalfloss.com
https://cards.fandom.com
http://plrplr.com
http://www.genetic-programming.org